
Michele Scacchi
Alpha Technologies
Optimizing your Mixing Process Using LAOS
Filler dispersion can affect many compound properties including strength, rebound, heat build-up, fatigue and cracking. What’s more, poor dispersion can cause poor processability, product failure and increased scrap costs. A traditional method of evaluating mixing efficiency utilizes the measurement of dynamic strain softening – also known as the Payne effect. Excellent, repeatable, reproducible Payne effect measurements can be made on Alpha’s Premier™ RPA.
That said, the Payne effect can have issues when describing the non-linear behaviour of rubber compounds. Fortunately, the application of Fourier Transformation to the shear stress signal is not only a powerful tool to quantify the level of long chain branching in polymers but also a very sensitive technique to optimize the mixing process of filled rubber compounds. This technique is called FT-Rheology.
FT-Rheology via Large Amplitude Oscillatory Shear (LAOS) reveals more information about the filler-filler / filler-polymer interactions and provides a check at the end of the mixing process to determine if the full dispersion of the filler in the rubber matrix has been achieved.
Non-linear thinking is great. Non-linear torque not so much.
In the non-linear region, the response of viscoelastic materials is no longer characterized by a sinus wave. The torque/stress signal is distorted: the higher the imposed deformation the more pronounced the distortion of the torque response, see Figure 1.
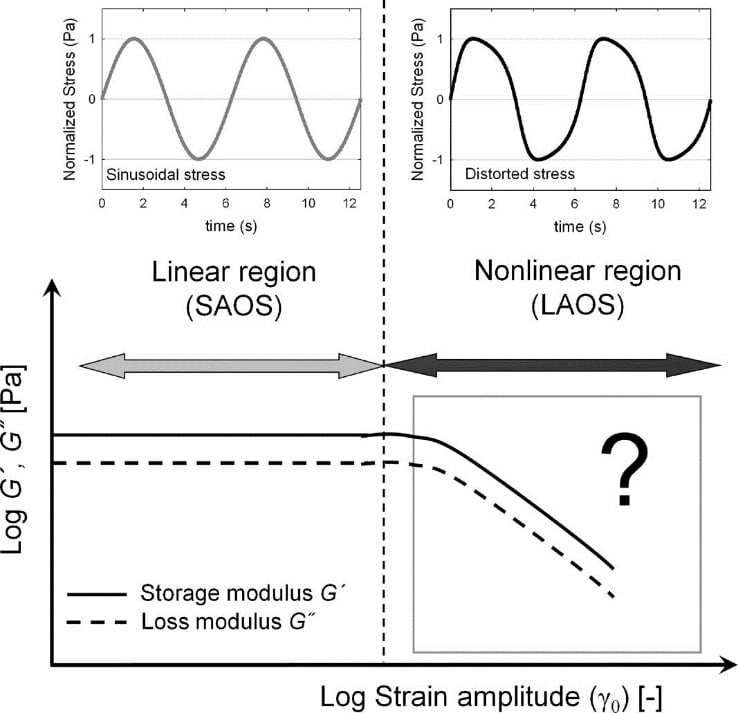
The only way to describe the real response of material tested in the nonlinear region (and quantify the distortion) is to apply FT-Rheology to account for all odd higher harmonics of the torque signal. In the comparison shown in the Figure 2, the torque was recorded without considering the contribution of higher harmonics (left) and then by considering all odd higher harmonics (right).
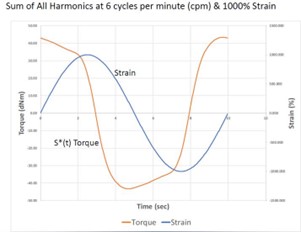
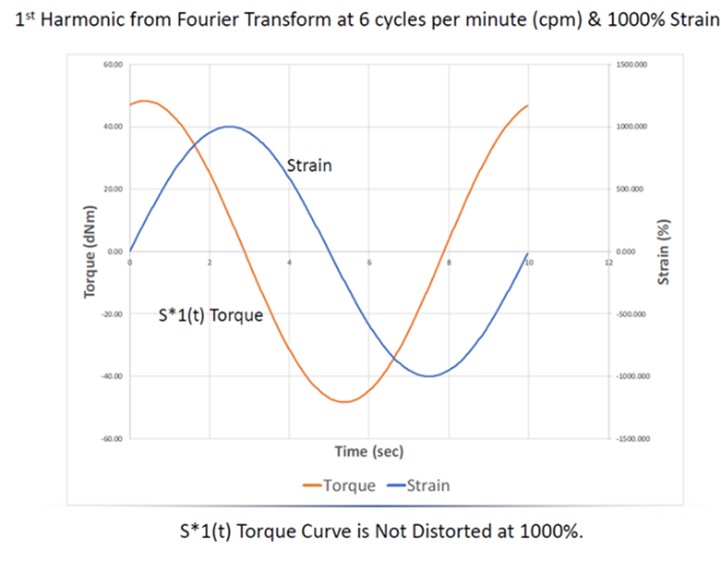
Figure 2: distortion the torque signal at large deformation
This approach was developed several years ago by A. Jeffrey Giacomin and John M. Dealy and is described in Techniques in Rheological Measurement (Chapman & Hall, 1993). According to this theory the shear stress signal can be described as a Fourier series, which is as the sum of all odd higher harmonics of Gʹ and G”, see Figure 3.
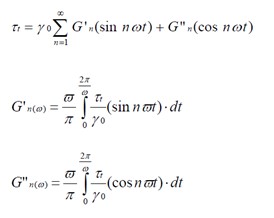
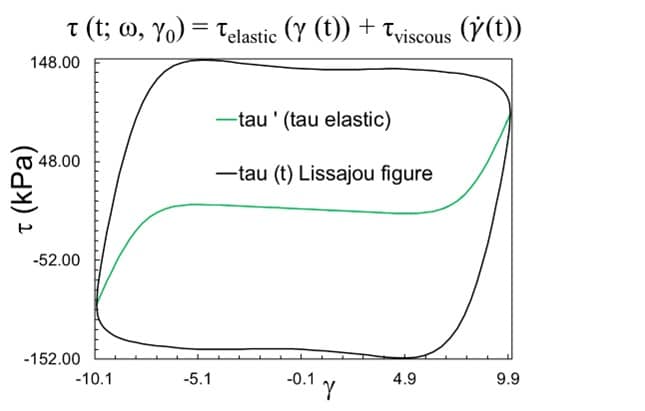
Typically, non-linear behavior of materials can be quantified by the ratio of the higher harmonics to the first, In/1 = I(nω1)/I(ω1) . The 3rd harmonic, In/1= I(3ω)/I(ω), has the highest relative intensity in comparison with the other odd harmonics (the following higher order terms typically decay rapidly), hence it is the most important in quantifying the non-linearity under LAOS. It was demonstrated that this ratio is the most sensitive to detect the filler/polymer interactions of rubber compound.
The LAOS technique is more accurate than the traditional Payne effect approach to describe the non-linear behavior of uncured rubber compound specially to evaluate the micro-dispersion of filler.
How to evaluate filler dispersion by LAOS technique.
One of the most interesting approaches used to study the complex set of events that occur along the mixing line with LAOS, was developed by Prof. Jean L. Leblanc.
Based on Leblanc’s model the non-linear response of uncured rubber compounds, expressed in terms of third relative torque harmonic, I3/1, vs. strain, can be described as the results of two combined effects:
- Effect due to the polymer component characterized by a sigma shape curve that becomes asymptotic to a straight line at high strain values
- Effect due to the filler component that it is characterized by a curve passing through a maximum and then tends to zero at high strain values.
Furthermore, Leblanc observed that all compounds during the mixing process show a local maximum located typically in the range between 400-600% of strain. The stronger is the filler-filler interaction the more pronounced is this local maximum, see Figure 4
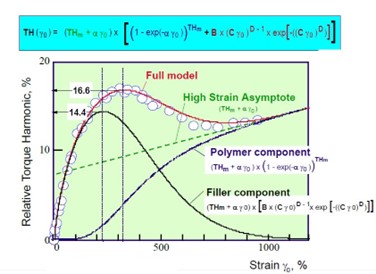
As the mixing process proceeds, less filler-filler interactions can be observed, which means that the filler network is significantly destroyed, and the local maximum is less and less pronounced. At the end of mixing if the full dispersion of the filler has been achieved the local maximum is almost vanished.
Therefore, the non-linear response of rubber compounds is dominated in the low range of strain by filler component, while in the high range of strain it is dominated by the polymer component.
That’s the theory and maths behind FT-Rheology via LAOS. Now let’s put it into practice. In Part 2 of this post, I will provide real examples of LAOS experiments to track the progress of filler dispersion along the mixing line.
References
- Leblanc, J.L.; Rubber Chemistry and Technology, 78, 54-75 (2005)
- Leblanc J.L., Chapelle C. de la; Rubber Chemistry and Technology, 76, 287 (2003)
- Leblanc J.L.; Rubber Chemistry and Technology, 86, 261–285 (2013)
- Leblanc J.L.; Journal of Applied Polymer Science 109, 1271 (2008)
- Nijman, G., Leblanc, J.L.; Journal of Applied Polymer Science 112, 942 (2009)
- Leblanc, J.L., Nijman, G.; Journal of Applied Polymer Science 112, 1128 (2009)
- Nijman, G.; GAK 68, 400 (2015)
Part 3: Using LAOS to Quantify Long Chain Branching and to Predict Processability
Michele Scacchi Alpha Technologies ICYMI – Recap for people who...
Read MorePart 4: Case Studies: Determination of Long Chain Branching in Polymer and Prediction of Processability
/*! elementor – v3.11.5 – 14-03-2023 */ .elementor-widget-image{text-align:center}.elementor-widget-image a{display:inline-block}.elementor-widget-image a...
Read MorePart 1: FT Rheology via Large Amplitude Oscillatory Shear (LAOS) – a five part series
Michele Scacchi Alpha Technologies Optimizing your Mixing Process Using LAOS...
Read MoreFinding Balance: Measure Cure & Blowing Reactions Using an RPA
Whether you are extruding or injection molding, the production of...
Read More





